Έχει σημειωθεί πρόοδος στη μελέτη της υπερταχείας κίνησης των οιονεί σωματιδίων Weil που ελέγχονται από λέιζερ

Έχει σημειωθεί πρόοδος στη μελέτη της υπερταχείας κίνησης των οιονεί σωματιδίων Weil που ελέγχονται απόλέιζερ

Τα τελευταία χρόνια, η θεωρητική και πειραματική έρευνα σχετικά με τις τοπολογικές κβαντικές καταστάσεις και τα τοπολογικά κβαντικά υλικά έχει γίνει ένα καυτό θέμα στον τομέα της φυσικής συμπυκνωμένης ύλης. Ως νέα έννοια της ταξινόμησης της ύλης, η τοπολογική τάξη, όπως και η συμμετρία, είναι μια θεμελιώδης έννοια στη φυσική συμπυκνωμένης ύλης. Η βαθιά κατανόηση της τοπολογίας σχετίζεται με τα βασικά προβλήματα της φυσικής συμπυκνωμένης ύλης, όπως η βασική ηλεκτρονική δομή του...κβαντικές φάσεις, κβαντικές μεταβάσεις φάσης και διέγερση πολλών ακινητοποιημένων στοιχείων σε κβαντικές φάσεις. Στα τοπολογικά υλικά, η σύζευξη μεταξύ πολλών βαθμών ελευθερίας, όπως ηλεκτρόνια, φωνόνια και σπιν, παίζει καθοριστικό ρόλο στην κατανόηση και τη ρύθμιση των ιδιοτήτων των υλικών. Η διέγερση από το φως μπορεί να χρησιμοποιηθεί για τη διάκριση μεταξύ διαφορετικών αλληλεπιδράσεων και τον χειρισμό της κατάστασης της ύλης, και στη συνέχεια μπορούν να ληφθούν πληροφορίες σχετικά με τις βασικές φυσικές ιδιότητες του υλικού, τις δομικές μεταβάσεις φάσης και τις νέες κβαντικές καταστάσεις. Προς το παρόν, η σχέση μεταξύ της μακροσκοπικής συμπεριφοράς των τοπολογικών υλικών που καθοδηγούνται από το φωτεινό πεδίο και της μικροσκοπικής ατομικής δομής και των ηλεκτρονικών τους ιδιοτήτων έχει γίνει ερευνητικός στόχος.

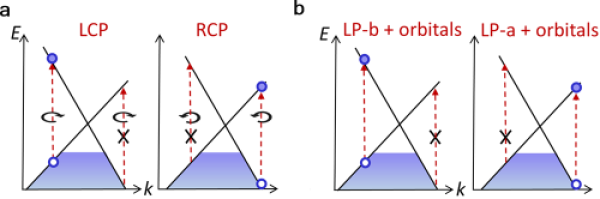
Η φωτοηλεκτρική συμπεριφορά απόκρισης των τοπολογικών υλικών σχετίζεται στενά με την μικροσκοπική ηλεκτρονική τους δομή. Για τα τοπολογικά ημιμέταλλα, η διέγερση του φορέα κοντά στην τομή των ζωνών είναι ιδιαίτερα ευαίσθητη στα χαρακτηριστικά της κυματοσυνάρτησης του συστήματος. Η μελέτη των μη γραμμικών οπτικών φαινομένων σε τοπολογικά ημιμέταλλα μπορεί να μας βοηθήσει να κατανοήσουμε καλύτερα τις φυσικές ιδιότητες των διεγερμένων καταστάσεων του συστήματος και αναμένεται ότι αυτά τα φαινόμενα μπορούν να χρησιμοποιηθούν στην κατασκευή...οπτικές συσκευέςκαι ο σχεδιασμός ηλιακών κυψελών, παρέχοντας πιθανές πρακτικές εφαρμογές στο μέλλον. Για παράδειγμα, σε ένα ημιμέταλλο Weyl, η απορρόφηση ενός φωτονίου κυκλικά πολωμένου φωτός θα προκαλέσει αντιστροφή του σπιν και, προκειμένου να επιτευχθεί η αρχή διατήρησης της στροφορμής, η διέγερση ηλεκτρονίων και στις δύο πλευρές του κώνου Weyl θα κατανεμηθεί ασύμμετρα κατά μήκος της κατεύθυνσης της κυκλικά πολωμένου φωτός, κάτι που ονομάζεται κανόνας χειραλικής επιλογής (Σχήμα 1).

Η θεωρητική μελέτη μη γραμμικών οπτικών φαινομένων τοπολογικών υλικών συνήθως υιοθετεί τη μέθοδο συνδυασμού του υπολογισμού των ιδιοτήτων της θεμελιώδους κατάστασης του υλικού και της ανάλυσης συμμετρίας. Ωστόσο, αυτή η μέθοδος έχει ορισμένα μειονεκτήματα: δεν διαθέτει δυναμικές πληροφορίες πραγματικού χρόνου για διεγερμένους φορείς στον χώρο της ορμής και στον πραγματικό χώρο και δεν μπορεί να δημιουργήσει άμεση σύγκριση με την πειραματική μέθοδο ανίχνευσης με χρονική ανάλυση. Η σύζευξη μεταξύ ηλεκτρονίων-φωνονίων και φωτονίων-φωνονίων δεν μπορεί να ληφθεί υπόψη. Και αυτό είναι κρίσιμο για την πραγματοποίηση ορισμένων μεταβάσεων φάσης. Επιπλέον, αυτή η θεωρητική ανάλυση που βασίζεται στη θεωρία διαταραχών δεν μπορεί να ασχοληθεί με τις φυσικές διεργασίες υπό το ισχυρό φωτεινό πεδίο. Η προσομοίωση χρονικά εξαρτώμενης λειτουργικής μοριακής δυναμικής πυκνότητας (TDDFT-MD) που βασίζεται στις πρώτες αρχές μπορεί να λύσει τα παραπάνω προβλήματα.

Πρόσφατα, υπό την καθοδήγηση του ερευνητή Meng Sheng, του μεταδιδακτορικού ερευνητή Guan Mengxue και του διδακτορικού φοιτητή Wang En της Ομάδας SF10 του Κρατικού Εργαστηρίου Επιφανειακής Φυσικής του Ινστιτούτου Φυσικής της Κινεζικής Ακαδημίας Επιστημών/Εθνικού Κέντρου Έρευνας του Πεκίνου για τη Φυσική Συμπυκνωμένης Ύλης, σε συνεργασία με τον καθηγητή Sun Jiatao του Τεχνολογικού Ινστιτούτου του Πεκίνου, χρησιμοποίησαν το αυτοαναπτυγμένο λογισμικό προσομοίωσης δυναμικής διεγερμένης κατάστασης TDAP. Διερευνώνται τα χαρακτηριστικά απόκρισης της διέγερσης quastipartid σε υπερταχύ λέιζερ στο δεύτερο είδος ημιμεταλλικού WTe2 Weyl.

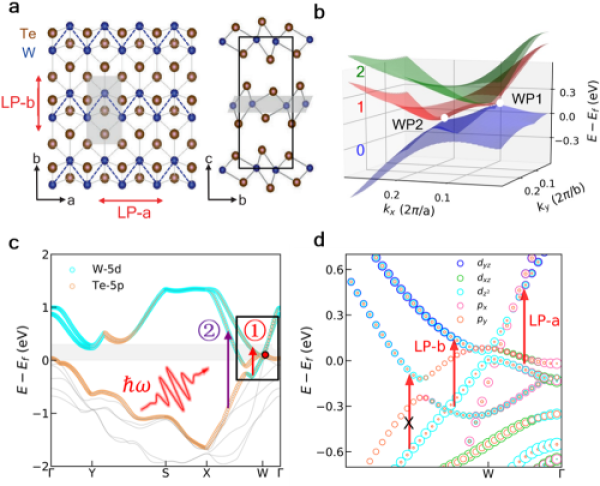
Έχει αποδειχθεί ότι η επιλεκτική διέγερση των φορέων κοντά στο σημείο Weyl καθορίζεται από την ατομική τροχιακή συμμετρία και τον κανόνα επιλογής μετάβασης, ο οποίος διαφέρει από τον συνήθη κανόνα επιλογής σπιν για τη χειρόμορφη διέγερση, και η διαδρομή διέγερσης μπορεί να ελεγχθεί αλλάζοντας την κατεύθυνση πόλωσης του γραμμικά πολωμένου φωτός και της ενέργειας των φωτονίων (ΣΧ. 2).

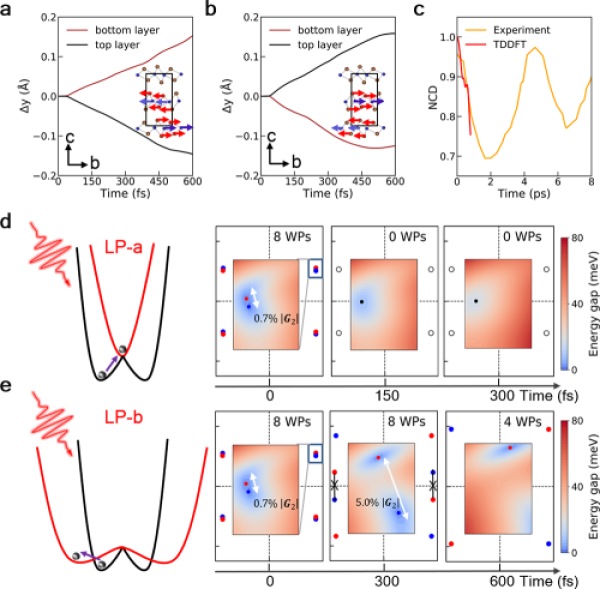
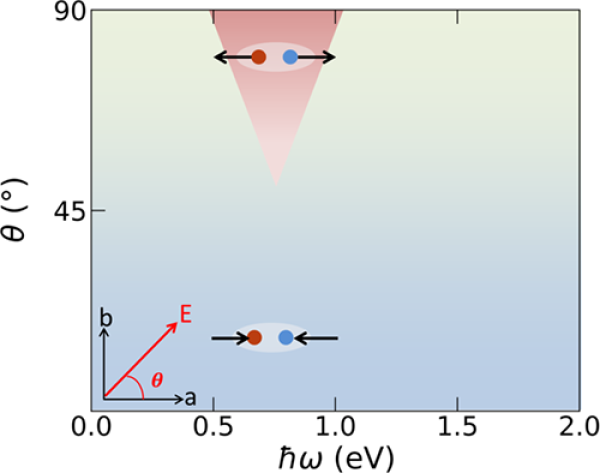
Η ασύμμετρη διέγερση των φορέων προκαλεί φωτορεύματα σε διαφορετικές κατευθύνσεις στον πραγματικό χώρο, γεγονός που επηρεάζει την κατεύθυνση και τη συμμετρία της ολίσθησης μεταξύ των στρωμάτων του συστήματος. Δεδομένου ότι οι τοπολογικές ιδιότητες του WTe2, όπως ο αριθμός των σημείων Weyl και ο βαθμός διαχωρισμού στον χώρο της ορμής, εξαρτώνται σε μεγάλο βαθμό από τη συμμετρία του συστήματος (Σχήμα 3), η ασύμμετρη διέγερση των φορέων θα επιφέρει διαφορετική συμπεριφορά των quasti-σωματιδίων Weyl στον χώρο της ορμής και αντίστοιχες αλλαγές στις τοπολογικές ιδιότητες του συστήματος. Έτσι, η μελέτη παρέχει ένα σαφές διάγραμμα φάσεων για τις φωτοτοπολογικές μεταβάσεις φάσης (Σχήμα 4).

Τα αποτελέσματα δείχνουν ότι η χειραλικότητα της διέγερσης του φορέα κοντά στο σημείο Weyl θα πρέπει να τύχει προσοχής και να αναλυθούν οι ατομικές τροχιακές ιδιότητες της κυματοσυνάρτησης. Τα αποτελέσματα των δύο είναι παρόμοια, αλλά ο μηχανισμός είναι προφανώς διαφορετικός, γεγονός που παρέχει μια θεωρητική βάση για την εξήγηση της μοναδικότητας των σημείων Weyl. Επιπλέον, η υπολογιστική μέθοδος που υιοθετήθηκε σε αυτή τη μελέτη μπορεί να κατανοήσει σε βάθος τις πολύπλοκες αλληλεπιδράσεις και τις δυναμικές συμπεριφορές σε ατομικό και ηλεκτρονικό επίπεδο σε εξαιρετικά γρήγορο χρονικό διάστημα, να αποκαλύψει τους μικροφυσικούς μηχανισμούς τους και αναμένεται να αποτελέσει ένα ισχυρό εργαλείο για μελλοντική έρευνα σε μη γραμμικά οπτικά φαινόμενα σε τοπολογικά υλικά.

Τα αποτελέσματα δημοσιεύονται στο περιοδικό Nature Communications. Η ερευνητική εργασία υποστηρίζεται από το Εθνικό Βασικό Σχέδιο Έρευνας και Ανάπτυξης, το Εθνικό Ίδρυμα Φυσικών Επιστημών και το Στρατηγικό Πιλοτικό Έργο (Κατηγορία Β) της Κινεζικής Ακαδημίας Επιστημών.

ΣΧ.1.α. Ο κανόνας επιλογής χειραλικότητας για σημεία Weyl με θετικό πρόσημο χειραλικότητας (χ=+1) υπό κυκλικά πολωμένο φως. Επιλεκτική διέγερση λόγω ατομικής τροχιακής συμμετρίας στο σημείο Weyl του b. χ=+1 σε γραμμικά πολωμένο φως.

ΣΧ. 2. Διάγραμμα ατομικής δομής του a, Td-WTe2. β. Δομή ζώνης κοντά στην επιφάνεια Fermi. (γ) Δομή ζώνης και σχετικές συνεισφορές ατομικών τροχιακών κατανεμημένων κατά μήκος γραμμών υψηλής συμμετρίας στην περιοχή Brillouin, τα βέλη (1) και (2) αντιπροσωπεύουν διέγερση κοντά ή μακριά από τα σημεία Weyl, αντίστοιχα. δ. Ενίσχυση της δομής ζώνης κατά μήκος της κατεύθυνσης Γάμμα-Χ

ΣΧ.3.ab: Απεικονίζεται η σχετική κίνηση μεταξύ των στρωμάτων της γραμμικά πολωμένης κατεύθυνσης πόλωσης φωτός κατά μήκος του άξονα Α και του άξονα Β του κρυστάλλου, και ο αντίστοιχος τρόπος κίνησης. Γ. Σύγκριση μεταξύ θεωρητικής προσομοίωσης και πειραματικής παρατήρησης. δ: Εξέλιξη συμμετρίας του συστήματος και η θέση, ο αριθμός και ο βαθμός διαχωρισμού των δύο πλησιέστερων σημείων Weyl στο επίπεδο kz=0.

ΣΧ. 4. Φωτοτοπολογική μετάβαση φάσης στο Td-WTe2 για γραμμικά πολωμένο διάγραμμα φάσης που εξαρτάται από την ενέργεια φωτονίων φωτός (?) ω) και την κατεύθυνση πόλωσης (θ)